Chapter 1 Review

1.1 Functions

Testing for functions

• The input value x is the number of representatives from a state and the output value y is the number of senators

Does the following equation represent y as a function of x?

                     

                     

 To each value of x there corresponds exactly one value of y.  So, y is a function of x

Evaluating a Function

Let 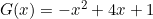    and find G(x+2)

 

 

 

Domain of a Function

• The domain of a function is the set of all values of the indpendent variable for which the function is defined
• If x is in the domain of   f, f   is said to be defined at x 
• If x is not in the domain of   f, f   is said to be undefined at x 
• The domain of a function can be described explicity or it can be implied by the expression used to define the function
• The implied domain is the set of all real numbers for which the expressions is defined

For instance:      

•  Another common type of implied domain is that used to avoid even roots of negative numbers

For instance:      

Evaluating a Difference Quotient

For   , find  

  
 




1.2 Graphs of Functions 

 
Max: 1
Min: 0.11 

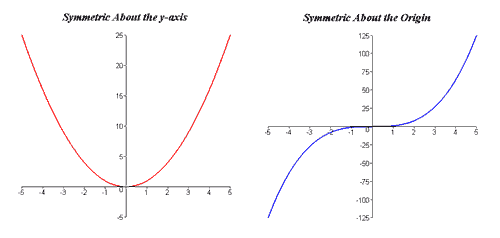
                    Even                                                Odd


Even and odd functions
This function is odd because:









This function is even because:




1.3 Shifting, reflecting, and stretching graphs




= the -1 means it shifts horizontally one unit to the right
= the -1 means it shifts vertically one unit down

1.4 Combinations of functions 
Just as two real numbers can be combined by the operations of addition, subtraction, multiplication, and division to form other real numbers, two functions can be combined to create new functions. 

Sum:   
                               
Difference:   
                                       
Product: 
                                 
Quotient:     


Identifying a composite function

Express the function as a composition of two function
                                       
=
=

1.5 InverseFunctions 

Finding inverse functions: 

Find the inverse of :   
                              
Verify that both:    and are equal to the identity function




Finding inverse functions algebraically

Find the inverse of: 


 
                                 Replace f(x) by y

                                  Interchange x and y
                                 Multiply each 
                               Isolate the y-term
                                Solve for y
                    Replace y by