is "f composed of g."
Now, for some examples:
Take f(x) = 2x+1 and g(x) = 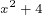 . Suppose we want to find
. Suppose we want to find (x)) .
.
First we would substitute what g(x) equals which is 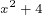 for "x" in the equation for f(x).
for "x" in the equation for f(x).
This would look like: f(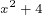 ) = 2(
) = 2(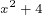 ) + 1. Now, we can solve the equation.
) + 1. Now, we can solve the equation.
f(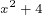 ) = 2
) = 2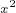 + 8 + 1.
+ 8 + 1.  Distribute
Distribute 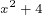 and 2.
and 2.
f(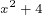 ) = 2
) = 2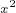 + 9
+ 9  Combine like terms.
Combine like terms.
Answer: f(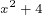 ) = 2
) = 2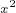 + 9.
+ 9.
What would happen if the composition of the function was(x)) ? The answer will be different in this case.
? The answer will be different in this case.
Substitute what f(x) equals which is 2x + 1 for "x" in the equation for g(x).
This would look like: g(2x + 1) =^{^2}) + 4. Now solve.
+ 4. Now solve.
g(2x + 1) = (2x + 1)(2x + 1) + 4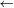 Set up FOIL.
Set up FOIL.
g(2x + 1) =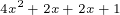 + 4
+ 4 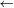 Use the FOIL method to distribute.
Use the FOIL method to distribute.
g(2x + 1) =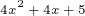
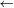 Combine like terms.
Combine like terms.
Answer: g(2x + 1) =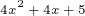
For any other information use this helpful website:
http://www.mathsisfun.com/sets/functions-composition.html
Also, this video shows other examples of how to do composition of a function:
This would look like: f(
f(
f(
Answer: f(
What would happen if the composition of the function was
Substitute what f(x) equals which is 2x + 1 for "x" in the equation for g(x).
This would look like: g(2x + 1) =
g(2x + 1) = (2x + 1)(2x + 1) + 4
g(2x + 1) =
g(2x + 1) =
Answer: g(2x + 1) =
For any other information use this helpful website:
http://www.mathsisfun.com/sets/functions-composition.html
Also, this video shows other examples of how to do composition of a function:
No comments:
Post a Comment