In other words... For every input (x) plugged into the equation, it will yield only one output (y) to make it a function.
Visual Representation of a Function...
Here we have an illustration showing that for every dot (value) in the x Set, there is only one match found in the y Set.
Visual Representation of a Non-Function
This picture illustrates how one dot (value) on the left is paired with more than one match on the right. This means that the input yielded multiple outputs which does not represent a Function.
Example... Is this a function?
The answer is yes, this is a function because every value in the x Set is paired with exactly one value in the y Set and not vice versa. Although 4 appears as both a positive and negative input and they both yield 16, this equation stays true to the definition of a function. On the other hand, if with another relationship positive 4 (x) were to yield positive and negative 16 (y), the equation would not be a function because the input would result in more than one output.
Functions can also be tested with the Vertical Line Test...
In functions, the equations are "single valued" so that again, no x value can have more than one why. This means that a vertical line should never end up crossing through a value more than once. If it does cross more than once, the equation that's been graphed is not a function.
On the top graph, the vertical line only runs through a value once. However, on the bottom graph the line runs through more than one points with the same x-value, hence not representing a function.
Functions can be presented in four ways...
1. Through a sentence describing the relationship between the inputs and outputs. (Verbal)
2. By a list or table revealing ordered pairs that satisfy the equation. (Numerical)
3. Points on a coordinate plane where x values are on the horizontal axis and y values are located on the vertical axis. (Graphical)
4. Through an equation revealing the relationship between two variables. (Algebraic)
Examples of each...
1. A tree grows 5 inches every year. The input value x is the number of years it has been alive. The output value y is the tree's height in inches.
2. {(1,5), (2,10), (3,15), (4,20), (5,25)}
3.
4. y = 5x
Example...
As well as testing to see if a relationship is a function... you can evaluate functions!
Let f(x) = x + 4 and find
a. f (2) b. f (w) c. f (x - 2)
Solutions
a. Replacing x with 2 in f(x) = x + 4 yields the following:
f(2) = (2) + 4 = 6
b. Replacing x with w in f(x) = x + 4 yields the following:
f(w) = (w) + 4 = w + 4
c. Replacing x with x - 2 in f(x) = x + 4 yields the following:
f(x - 2) = (x - 2) + 4 = x - 2 + 4 = x + 2
Functions can be represented...
2. sin, cosine and tangent
3. and many, many more but we're just sticking to the basic ideas of functions!
Domain and Range...
Domain and Range play a very big role in deciding whether an equation is or is not a function.
1. Domain:
- The values that go into a function
- The inputs
- The x-values
- The independent variables
2. Range:
- The values that come out of a function
- The outputs
- The y-values
- The dependent variables
Functions also include...
Here are some videos to help with these topics expanding on the basic function...
1. Piecewise-Defined Functions
(Evaluating Piecewise-Defined Functions)
(Graphing Piecewise-Defined Functions)
2. Even and Odd Functions
(Explaining if a Function is Even, Odd or Neither)
3. Absolute Value Functions
(Explaining and Graphing Absolute Value Functions)
(Graphing Absolute Value Functions)
Websites for Extra Help...
1. http://www.mathsisfun.com/sets/function.html
2. http://www.freemathhelp.com/functions.html
3. http://www.mathwarehouse.com/algebra/relation/math-function.php
4. http://www.purplemath.com/modules/fcns.htm
Videos for Extra Help...
Julia G, 2nd Hour Wilhelm Pre-Calculus A










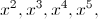

No comments:
Post a Comment