If (x, y) is a point on the unit
circle of the first quadrant, then x and y are the lengths of the sides of a
right triangle whose hypotenuse has length 1. So, for the Pythagorean theorem:
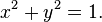
The trigonometric
functions sine and cosine can be defined on the unit circle as follows:
The unit circle is the
locus of points of the plane having a distance less than or equal to the unit
from the center of the circle. So:
-1 ≤ y ≤ 1 and
-1 ≤ x ≤ 1
From here we are able to
determine the domain of sine and cosine in the unit circle:
-1 ≤ sin (t) ≤ 1 and -1
≤ cos (t) ≤ 1
The unit circle provides
an intuitive way to view the sine and cosine as periodic functions with the
identities:
*( for every integer
k)
These identities result from the fact that the coordinates x and y of a
point on the unit circle remain the same increasing or decreasing the angle t
for any number of turns (1 turn = 2π radians).
And here they are for every quadrant.
With the correct sign* (plus or minus) as per Cartesian Coordinates.
Note that cos is first and sin is second, so it goes (cos, sin):
And in radians:
*And this is the trend of the sign of sine and cosine in
the unit circle:
But sine and cosine are not
the only functions of the real variable t.
Below you can see
the six trigonometric functions of t :
Evaluating
Trigonometric Functions Using the Unit Circle:
It is important to recognize the radian measure of the
standard angles related to:
located in
quadrants II, III, and IV.
Here there
is a useful video about the evaluation of trigonometric functions:
Other Facts Derived From the Unit Circle:
sin(−θ)
= −sin(θ )
Therefore sin(θ ) is an odd function, as well as functions csc, tan and cot.
While functions cos and sec are even
functions.
Marco Salvatore
