Horizontal and Vertical Asymptotes

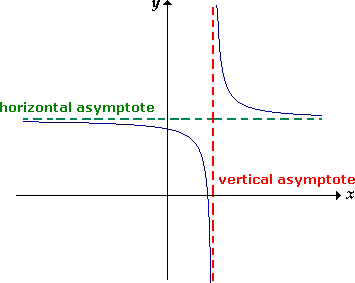
Vertical and Horizontal Asymptotes

Asymptote- An asymptote is a line or curve that approaches a given curve arbitrarily closely.

Definition of vertical and horizontal asymptotes



Vertical asymptote- The line x=a is a vertical asymptote of the graph of f if f(x)→ ∞ or f(x)→ -∞ as x→ a, either from the right or from the left

Horizontal asymptote- The line y=b is a horizontal asymptote of the

graph of f if f(x)→b as x→∞ or x→ -∞

Finding Horizontal and Vertical Asymptotes

To Find Horizontal Asymptotes:

1) Put equation or function in standard form.

2) Remove everything except the biggest exponents of x found in the numerator and denominator.

Examples:

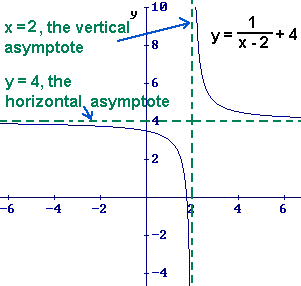
 Find the horizontal asymptotes of:

In order to figure out what the horizontal asymptote is, you must look at the largest degree exponent found in both the numerator and the denominator. Then, you must look at the leading coefficients for both the numerator and denominator and turn it into a fraction.

 

In this case, 2/3 is the horizontal asymptote of the above function. You should actually express it as y=2/3. This value is the asymptote because when we approach x=infinity, the function will always get closer and closer to y=2/3. Here's a graph of that function:

Shortcuts:

• If the exponent in the denominator of the function is larger than the exponent in the numerator, the horizontal asymptote will be y=0, which is the x-axis.
• If there is a bigger exponent in the numerator of a given function, then there is NO horizontal asymptote. For example:

In this function, the 3 is greater than the 2 so there is no horizontal asymptote

Finding Vertical Asymptotes 

1. Find the values that make the deominator equal 0

2. If any of those values don't make the numerator 0, then they are vertical asymptotes

Example:

look at the denominator in this function and set it equal to zero

3-9=0

 solve the equation  

 3 =9

=3

 x=1.44

So, the grapg of this function will have a vertical asymptote at x=1.44

Finding intercepts, vertical and horizontal asymptotes

Start with the given equation

 

Subtract x from both sides
 

  Factor out the

Divide both sides by

Y Intercept:

To find the y-intercept, plug in

Simplify

Take the square root of both sides
or Simplify
So the y-intercepts are (0,) and (0,)

X intercept Go back to the original equation

To find the x-intercept, plug in

Square 0 to get 0
Multiply both sides by 4-x
Multiply
Add x to both sides

So the x-intercept is (1,0)

Asymptotes To find the vertical asymptote(s), simply set the denominator equal to zero

Solve for x
So the vertical asymptote is at
Go back to the original equation

Rearrange the terms

Notice how the coefficient of x for the numerator and denominator is -1. So the horizontal asymptote is the ratio . Since we are dealing with a square in , this means that the final equation looks like . So there are two final parts and

This means that there is symmetry with respect with the x-axis and that there are two horizontal asymptotes and

 

Extra Help

blog post by: Connor Saeli