Let's start off with a basic book definition:
Remainder Theorem: Says if a polynomial f(x) is divided by x-k, the remainder is r =f(k)
To understand this better lets look at a sample problem.
Evaluate the following function at x=3

So, to solve this problem you could use long division to divide the function by (x-3), but a far easier method would be to use synthetic division.
If you need a reminder on how to solve using synthetic division take a quick glance at this video.
http://www.youtube.com/watch?v=bZoMz1Cy1T4

3│5    2    -14    5

  │      15   51   111

  │________ 

     5   17    37   116

 

 

So after solving it by synthetic division, you get a remainder of 116 or r=116.  Using the definition previously stated, f(3) = 116.  This also will mean that the point (3, 116) will be a point on the function:

's graph

To wrap up, the remainder of a potential factor (116 in our example) of a function, can be wxpressed as a value at that function.  The remainder will have a place on the y- axis of the graph when the function is at that specific x value (3 in our example).

The Factor Theorem- A polynomial f(x) has a factor (x- k) if and only if f(k). 
So what did that all mean? Basically a potential factor must be able to divide evenly into a polynomial, meaning that there will be no remainder and, yes f(k)= 0.  Let's dwelve into an example to investigate the matter furthur.

If you roll your time clocks back to when you were a  innocent little freshman, you probably saw problem likely looked something like this:
 = f(x)
And then of coarse you would see that this easily factored and would soon write (x +5), (x-4) and use the zero- product property to determine the zeros of that function were x= -5, 4.

The Factor Theorem works in a similar way in that you have to work backwards.  Now normally you would just multiply (x +5), (x-4) together to see that it equaled = f(x).  Unfortunately in this polynomial: , as you can see by its lead coefficient (4), that it has more than two factors (it has 4), and knowing two solutions will not help you solve the problem.

A problem dealing with this polynomial might look something like this:
Determine whether (x+3) and (x+4) are factors of the function f(x)=

You might look at this function on test day and wonder if there is some typing error because there is no x³ term visible.  Rather than exclude it, which we shouldn't do because it is mean, we simply put the coefficiant 0 in place of it, re-writing the polynomial as
 
Like above, we will use synthetic division to determine if -3 and -4 are factors (remember to take the opposite of the (x+3) and (x+4) because they are inside parenthesis!)

 

-3│1  0 -15 -10 24

   │    -3  9   18 -24

   │________

      1  -3  -6  8  0

 

 

Solving this out, you can see that -3 is indeed a factor of the function above because there is no remainder, or f(-3)= 0
The new polynomial is written as .  Since (x + 3) is a factor, if you multiply the two together, you should (and will) get the original function: . 

Now let's test out if -4 works:

-4│1   0     -15    -10   24

   │    -4      16      4     24

    │____________

      1  -4      -1     -6     48

 

 

What's This? The new function has a remainder of 48 (Remember to Add and not subract the 24's at the end!!).  According to The Factor Theorom, f(k) must =0 and
 , meaning that (x+4) is NOT a factor of

Rational Root Therom: Says that if f(x)= 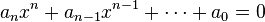 has integer coefficients, every rational zero of f has the form that rational zero=

Now what could all of this possible mean?
Its simply the factors of the constant term divided by factors of the leading coefficient
That's simply written as:

Let's put this into an example problem:
Find the rational zeros of:
 = f(x)

Well first, you must find the rational zeros; we know they are factors of 15, the constant term divided by  or the factors of:


So the factors of 15 are: 1,3,5, and 15
The factors of   (use 1, the lead coefficient): just 1 (that was easy wasn't it :)
So the rational roots will be:

Remember to include both the negative and positive numbers when determining rational roots (because negative numbers are rational too!)
Now you COULD test out all 8 of these values out by synthetic division to see which zeros fit, but there is a much simpler way.  Notice the coefficient's of the equation: 1+1-17+15.  Notice how they add up to 0.  This means that 1 will be a rational root, but let's double check to make sure using synthetic division.

 

1│1    1   -17   15

│         1    2    -15

│____________

     1    2    -15    0

 

 

Using The Factor Theorom, since there is a remainder of 0, 1 is indeed a rational zero of
 = f(x)
With (x-1) factored out the new equation is as follows:

And now you can easily factor it out: (x-3), (x+5)
to determine the other rational zeros: 3 and -5 (along with 1)
All of the rational zeros will be 1,3, and -5

Rational Root theorom help:
http://www.youtube.com/watch?v=GTx-rXTQg1o

Jacob Sandy

2nd Hour

10/8/12