Graphing Rational Functions

Here is a definition of a Rational Function:
-A function that is the ratio of two polynomials but the polynomial you are dividing cannot be by 0.

-The equation below is rational because one is being divided by the other, like a ratio.

 -To graph a rational function, you first need to find the asymptotes and intercepts, plot a few points, then sketch the graph.

Graph the following:

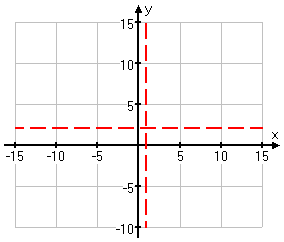
         Vertical Asymptote:

x – 1 = 0
x = 1


Horizontal Asymptote:


 y = ²/₁ = 2
y=2


- You need to then plot the asymptotes with dashed lines on the graph. 


X-Intercept: 

x = 0:  y = ^{(0 + 5)}/_{(0 – 1)} = ⁵/_–1 = –5  
X=-5 


Y-Intercept:

  0 = 2x + 5
        –5 = 2x
     –2.5 = x

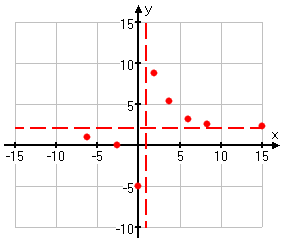
- Now I'll pick a few more x-values, compute the corresponding y-values, and plot a few more points.

x	y = (2x + 5)/(x – 1)
–6	(2(–6) + 5)/((–6) – 1) = (–12 + 5)/(–7) = (–7)/(–7) = 1
–1	(2(–1) + 5)/((–1) – 1) = (–2 + 5)/(–2) = (3)/(–2) = –1.5
2	(2(2) + 5)/((2) – 1) = (4 + 5)/(1) = (9)/(1) = 9
3	(2(3) + 5)/((3) – 1) = (6 + 5)/(2) = (11)/(2) = 5.5
6	(2(6) + 5)/((6) – 1) = (12 + 5)/(5) = (17)/(5) = 3.4
8	(2(8) + 5)/((8) – 1) = (16 + 5)/(7) = (21)/(7) = 3
15	(2(15) + 5)/((15) – 1) = (30 + 5)/(14) = (35)/(14) = 2.5

-Here is what the graph looks like with the plotted points:
 




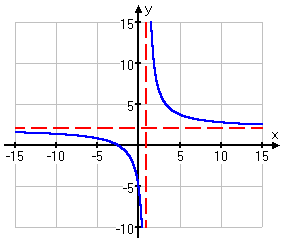
-Here is what the graph should look like: