The Fundamental Theorem of Algebra

The Fundamental Theorem of Algebra

Definition: If the f(x) is a polynomial of degree when n > 0, f has at least one zero in the complex number system

• The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root

• 
  
  In the complex number system, every nth-degree polynomial function has precisely n zeros
  
  
  • Complex Numbers: adding real numbers to real multiples of the imaginary unit, such as i
   Example of finding zeros of a polynomial function
•  Steps:
  1. Factor out
  2. Factor x^2+4
  3. Write the polynomial as a product of linear functions
  4.  list the zeros left in the parenthesis     
  
  
  
  
   
  
  

  

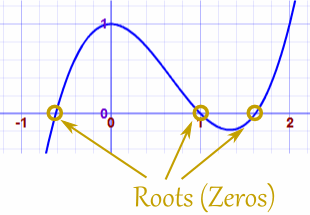
  A root (zero) is where the polynomial is equal to zero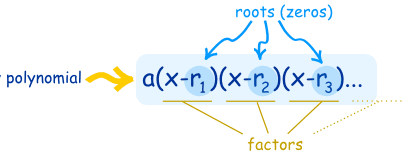

  

  Polynomials can be written in this form as well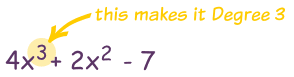

  

  This is because it is the highest degree in the polynomial equation
  
  
  
  

   

  Example: Find the roots of x^2-9

  
  

  step one:  Add 9 to each side    x^2=9

  
  

  Step two: Take the square root of each term x =3, x =-3

  
  

  Extra help, checkout these sites and videos for better and further explanations

  1. Polynomials-Fundamental Theorem of Algebra 
  2. Finding complex zeros of a polynomial function 
  3. Fundamental theorem of algebra explanation  
  4. Daves crash course of complex numbers in The fundamental Theorem 

   

   

  
  

  
  

   

  
  

  
  

  
  

  
  

  
  

  
  
  
  
  
  
  
  
  
  
  

  
  

  
  

   

  
  

  
  

  
  

   

-Alec Tropea