Pre-Calculus A 2nd Hour, Fall 2012: Complex Numbers and Their Conjugates

Having difficulty with complex numbers? Have no fear! They are actually quite easy to grasp once you understand the definition. Here it is:

Definition: a number of the form a+bi where a and b are real numbers and i is the square root of -1.

Standard form: a + bi

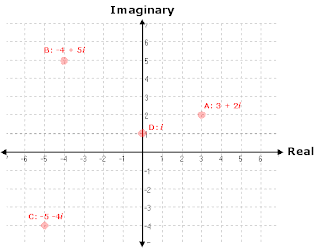
Heads up ---> Imaginary numbers ( i ) are not graphed on the x or y axes. Instead, we call the y axis the Imaginary Axis and the x axis the Real Axis.

Example: A) Graph the following points: (0,0) (1,2) (2,4)

B) Graph the following points: (-4+5i) (3+2i) (-5-4i)
Note: This is the same as saying that (-4, 3, and -5) are plotted on the real axis and (5i, 2i, and -4i) are plotted on the imaginary axis.

This means that when adding or subtracting, you add or subtract real and imaginary parts of the numbers separately.

Example: Add or subtract where necessary.
                     A) (3-i) + (2+3i)

              First remove the parentheses and multiply the +1 through the second complex number--->
                                       3 - i + 2 + 3i
              Then combine like terms (Real numbers with real numbers and imaginary numbers with imaginary     numbers)--->
                                      (3+2) +(-1+3)i
              Then write the equation in standard form--->
                                      5 + 2i
                      B) 3-(-2+3i)+(-5+i)

              Again, remove the parentheses and multiply the -1 and +1 through the first and second complex numbers--->
                                      3 + 2 -3i - 5 +i
              Combine like terms--->
                                      3 + 2 - 5 -3i + i
              Write in standard form--->
                                     0 - 2i
                                      -2i

When multiplying complex numbers together, you distribute or use foil.

Example: Multiply and write in standard form.
             A) (2-i)(4+3i)
   Use foil to distribute the (2-i) through the (4+3i)--->

Then combine like terms (WAIT! Think. Can anything be simplified first? You are correct!

= -1) --->
                                                             8 + 2i - 3(-1)
                     Now combine like terms and write in standard form--->
                                                                 8 + 2i +3
                                                                   11+2i
When dividing complex numbers, you MUST remember to multiply by the denominator's conjugate. What is a conjugate you ask? A conjugate is the opposite of whatever equation you have. For example, the conjugate for a+bi would be a-bi.

Try this: Divide the two complex numbers.